 Верите ли вы в то, что после крупного везения всегда наступает полоса неудач? Например, если сегодня в покере вам пришел действительно сильный расклад, то завтра вас будет игнорировать даже аппарат по выдаче бахил. А может вы думаете, что ваш талант к выпиливанию лобзиком или ваша неземная красота обязательно должны передаться по наследству вашим детям? Если вы в этом уверены, то статистика высказывается по этому вопросу более сдержанно. Объяснить подобные явления поможет статистический принцип под названием “регрессия к среднему”. Его игнорирование может привести как минимум к плохому настроению, а как максимум – к полному разочарованию в своей жизни. На самом деле идея очень проста. Разберем ее.
Верите ли вы в то, что после крупного везения всегда наступает полоса неудач? Например, если сегодня в покере вам пришел действительно сильный расклад, то завтра вас будет игнорировать даже аппарат по выдаче бахил. А может вы думаете, что ваш талант к выпиливанию лобзиком или ваша неземная красота обязательно должны передаться по наследству вашим детям? Если вы в этом уверены, то статистика высказывается по этому вопросу более сдержанно. Объяснить подобные явления поможет статистический принцип под названием “регрессия к среднему”. Его игнорирование может привести как минимум к плохому настроению, а как максимум – к полному разочарованию в своей жизни. На самом деле идея очень проста. Разберем ее.
Талантливость или гениальность, крупное везение, провал или другое экстраординарное явление встречаются крайне редко, то есть вероятность их возникновения чрезвычайно мала. Вероятность повторения столь редкого события будет еще меньше, так как для ее нахождения используется умножение вероятностей. Таким образом, после любого экстремального события (плохого или хорошего) все возвращается на круги своя. Здесь очень важный момент – жизнь НЕ компенсирует ваши неудачи или победы, просто ваши показатели везения устремляются к своим средним значениям. Это и есть регрессия к среднему (от лат. regressio — обратное движение). То же самое происходит и при смене поколений. Ваши дети обязательно будут талантливы, но, вероятнее всего, в другой области.
Впервые понятие регрессии ввел сэр Френсис Гальтон, английский исследователь широкого профиля. На его счету еще одно основополагающее понятие статистики – корреляция. Изучая наследственность, Гальтон измерял у своих соотечественников все, что можно было измерить: головы, носы, руки, количество суетливых движений, степень привлекательности и т.д. Гальтон считал, что характер человека, его умственные способности и талант также определяются наследственностью и подчиняются принципу нормального распределения.
В одной своей работе он пытался найти связь между ростом родителей и ростом их детей. Зависимость очевидна – у высоких родителей рождаются высокие дети и наоборот. Но Гальтон, помимо этого, обнаружил также не совсем логичные закономерности. Например, он обнаружил, что у родителей с ростом выше среднего были высокие дети, но они были не такими высокими, как их родители. А у родителей с ростом ниже среднего дети были низкие, но не ниже своих родителей. Это означает, что рост уже взрослых детей отклоняется в меньшей степени от среднего значения, чем рост родителей. То есть, потомки сильнее «регрессируют» к среднему. Вообще-то Гальтон назвал это явление “регрессией к посредственности”, что более точно отражает смысл, ИМХО.
Гальтон построил график, напоминающий современную диаграмму рассеяния.

Он разбил людей по группам в зависимости от их роста (в дюймах), для каждой группы рассчитал среднее арифметическое и отметил эти значения на графике. Далее Гальтон аппроксимировал эти точки и построил прямые, так называемые линии регрессии. Гальтон даже рассчитал коэффициент корреляции – 2/3. Это значит, что всего на 67% рост детей определяется ростом родителей.
На графике подписано: “Когда средний рост родителей больше среднего из популяции, дети обнаруживают тенденцию быть ниже своих родителей. И наоборот, когда средний рост родителей меньше среднего из популяции, дети обнаруживают тенденцию быть выше своих родителей”.
Хотя сейчас выводы и идеи Гальтона не критикуют, а мягко подвергают сомнению, они имеют революционное значение для статистики. Благодаря этому разностороннему ученому в настоящее время широко используются регрессионный и корреляционный анализы.
Ниже нами построена диаграмма рассеяния (она же точечная диаграмма) для данных, собранных Гальтоном. В 1886 году он представил табличку, где был указан рост 928 уже взрослых детей и рост их 205 родителей (средневзвешенное значение роста отца и матери). С тех пор эти данные часто используют как отличный пример регрессии к среднему. 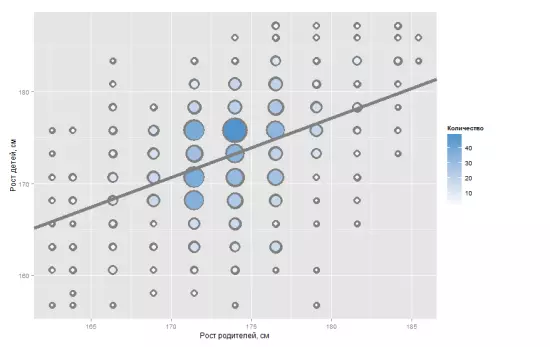


Да, тенденции к усреднению очень сильны во многих сферах. Однако! В статье почему то умалчивается, что СРЕДНЕЕ – НЕСТАБИЛЬНО. Среднее может как увеличиваться, так и уменьшаться. Если бы этого не было, то появление гигантсиких динозавров было бы невозможно и люди бы не выросли за тысячу лет чуть ли не на 30 см. в среднем..
Поэтому тех, кого расстроила статья относительно везения/невезения спешу утешить – во=первых законы среднего работают НЕ ВО ВСЕХ СИСТЕМАХ. Во-вторых человек – мыслящее и деятельное существо, которое в большинстве сфер своей деятельности может сознательно влиять на величину среднего :-)))